O que as Redes Neurais fazem exatamente para aprender?
Vamos mergulhar na profundidade das Redes Neurais?
Nesse texto aqui falamos um pouco sobre formas de se detectar faces usando uma combinação de Histograma de Gradientes Orientados com Máquinas de Vetores Suporte. É um bom jeito de se detectar faces, principalmente quando precisa-se de rapidez de processamento e o hardware não é tão poderoso assim.
No entanto, Deep Learning é Deep Learning e vice-versa. Falando sério, muito do que se sabia de reconhecimento de objetos mudou (para melhor) com a popularização das redes neurais com múltiplas camadas. Como estamos numa jornada para entender todo o processo, precisamos compreender melhor o que as redes neurais fazem para serem tão boas no que fazem.
Introdução às Redes Neurais Artificiais
Modelos matemáticos e computacionais que se inspiram em redes neurais biológicas já são propostos na literatura desde os anos 40. O próprio pai da Computação, Alan Turing, propôs uma tal de "B-type unorganised machine" que, na prática, já seria um neurônio artificial.
Tá, mas qual o sentido de modelar algo que possui similaridades com o cérebro de humanos e animais? É para brincar de Deus ou coisa do tipo? Já digo que não e explico o motivo.
Essa estrutura computacional mostrou-se muito útil para determinar padrões e "aprender" com os dados de entrada de maneira automatizada. Não é possível ainda ir longe na comparação da rede neural artificial com a biológica, pois enquanto nosso cérebro nos possibilita trabalhar com múltiplas tarefas (até criar novas!), cada rede neural artificial projetada possui uma finalidade muito específica. Isso nos tranquiliza no sentido de que, por um bom tempo, elas não vão se rebelar e escravizar humanos.
Por enquanto não temos que nos preocupar com isso.
Para começar a mergulhar no mundo das redes neurais, precisamos discutir quais são os neurônios artificiais mais usados. Para começo de conversa, precisamos falar do perceptron e dos neurônios sigmoidais. Eles não são muito usados em Deep Learning, mas para ter um entendimento mais completo sobre o assunto, precisamos conhecê-los.
Pelo nome parece complicado, mas o perceptron é uma ideia bastante simples. Você pode entendê-lo como uma função que recebe um ou mais valores (por enquanto assuma que eles sejam a, b e c) e, ao final, uma saída vai apresentar um valor binário 0 ou 1, dependendo desses valores.
Representação muito simples de um perceptron.
A ideia do perceptron é receber um conjunto de valores de entrada (no exemplo são a, b c, mas poderia ser mais), fazer uma conta com eles e se esses valores ultrapassarem um determinado valor (que chamaremos de limiar) então a saída será 1. Do contrário, teremos 0.
Se você pensar que um perceptron é um modelo que simula um único neurônio, se essa conta for maior do que o limiar, esse neurônio dará saída 1 e vai "disparar" (assim como o neurônio biológico "dispara" um impulso elétrico no nosso cérebro para estabelecer comunicação com outros neurônios). Se for 0, nada acontece.
Isso que eu apresentei é o que esse neurônio artificial bastante simples faz. Eu até fiz um vídeo mais antigo em que eu uso um show da Anitta como exemplo (com números e tudo mais) para explicar as contas por trás de um perceptron. É meio antigo, mas acho que você vai gostar e te ajudará a entender =)
Eu e meus exemplos para explicar coisas rsrs
Só que eu mencionei lá em cima um tal de neurônio sigmóide. Mesmo em Redes Neurais simples, prefere-se ele ao perceptron. Por quê? Respondendo de maneira simples e direta: o perceptron é muito sensível. As vezes uma pequena mudança em um valor de entrada faz com que a saída mude de 0 para 1.
Explicando esse problema, imagine que vamos usar um perceptron para modelar uma situação típica do cotidiano: comprar um carro. Se o neurônio "disparar", significa que o carro será comprado. Se não, então nada de carro.
Nesse exemplo, os valores de entrada do perceptron poderiam ser as economias de uma pessoa para adquirir esse veículo que, por exemplo, custa 50 mil reais (que se torna o limiar daqui). Faz sentido o neurônio "disparar" 1 se as economias forem bem superiores aos 50 mil reais.
Faz sentido que com 49 mil reais de economia, a pessoa não compre o carro. Aumentando em dois mil reais, dá R$51.000,00 e a pessoa compra. Só que será que isso faz sentido? Você usaria praticamente todas as suas economias para comprar um carro e ficaria com pouco para se resguardar? Se você é cuidadoso com suas economias, é provável que não faria isso.
Se você tem 80 mil ou 65 mil, faz sentido comprar pois você tem um “colchão” maior. Com 51 mil, não é tão bom assim. Assim, o poder de decisão do perceptron é 8 ou 80. Precisamos de algo mais suave.
Para criar uma modelagem mais flexível, surgiu o neurônio sigmóide. Falemos dele.
Neurônio Sigmóide
A função usada nesse neurônio não tem um efeito tão severo na saída de acordo com a variação na entrada. Como vimos, uma pequena mudança de uma entrada que já computava um valor próximo ao limiar faz com que a saída do perceptron mude de 0 para 1 (ou vice-versa). No caso do neurônio sigmóide, por ele usar a função logística, ele permite uma mudança mais gradual.
Para entendermos, vamos olhar novamente a função usada pelo perceptron (que em inglês chamamos de step function) e comparar com a função logística do neurônio sigmóide.
Na função usada pelo perceptron, imagine que o eixo X continue a ser o salário. Note que quando ultrapassamos os 50 mil reais de salário, a saída do perceptron que era 0 (não comprar o carro) muda para 1 (comprar o carro). São apenas duas saídas possíveis, representadas no eixo Y.
Vamos aplicar a mesma lógica para o neurônio sigmóide (imagem abaixo). Agora, ao invés de termos apenas duas saídas para uma enorme gama de salários, temos um intervalo de números fracionários entre 0 e 1. Esses valores indicam a probabilidade de se comprar o carro. Se o nosso salário é de aproximadamente R$ 50.000,00 (círculo vermelho), aí a probabilidade de compra é de 50% (0,5). No círculo verde, temos um salário de 60 mil reais e aproximadamente 70% de possibilidades de comprar o carro. Assim, com uma função logística, temos uma saída muito mais rica de informações do que apenas 0 e 1.
Representação da função logística que modela as saídas de nosso neurônio sigmóide capaz de modelar a situação de adquirir um carro.
Agora que temos um neurônio “mais espertinho”, saiba que ainda temos uma estrutura computacional simplificada. O verdadeiro poder da rede neural biológica são as conexões entre neurônios possibilitadas pela sinapse. Algo parecido precisa ocorrer nas arquiteturas de redes neurais artificiais.
Arquitetura de Redes Neurais
Redes neurais capazes de fazer algo mais impactante precisam conectar seus neurônios de alguma forma, até para "distribuírem" esses dados entre mais unidades de processamento, que são os neurônios.
Para entendermos melhor, vamos primeiro compreender as estruturas de uma rede neural mais complexa. A imagem abaixo, por exemplo, apresenta uma rede neural com 3 camadas, sendo uma delas denominada oculta.
Típica rede neural com múltiplas camadas (chamada de rede neural feedforward na literatura).
Para ajudar na identificação, eu colori alguns neurônios. Os que estão pintados de azul fazem parte da camada de entrada. Essa camada apenas introduz dados para a rede, sem fazer computação dos dados propriamente dito.
Apesar do nome misterioso, as camadas ocultas (com os neurônios pintados de verde) fazem um trabalho que mencionamos agora a pouco: processamento de dados, que aqui são transmitidos pela camada anterior. Isso é feito aplicando a função de ativação (computar os valores de entrada em uma função como é o caso da logística), "passando para frente" os dados para a próxima camada. A "camada da frente" pode ser outra camada oculta ou a camada de saída.
A camada de saída só apresenta o resultado final da rede, que pode ser tanto dizer se a pessoa vai comprar algo como um carro ou informar que uma foto possui um cachorro ou uma face humana.
Finalmente, é importante dizer que uma rede neural pode ter uma ou mais camadas ocultas, enquanto só é possível ter uma única camada de entrada e uma única camada de saída.
Dito isso, é importante falarmos sobre os as arquiteturas básicas mais conhecidas de redes neurais: os perceptrons de camada única e os perceptrons multicamada.
As arquiteturas do primeiro tipo já vimos: elas possuem um único neurônio, sem usufruir de camada de entrada, saída ou mesmo oculta. Nesse caso, o neurônio sozinho "acumula as funções". Elas são basicamente uma rede com um único perceptron ou neurônio sigmóide (é importante dizer que a literatura chama essa arquitetura de perceptron de camada única mesmo que o seu neurônio propriamente dito não seja um perceptron ¯\_(ツ)_/¯).
Agora, os perceptrons multicamada possuem uma ou mais camadas e possuem diversas aplicações no cotidiano (inclusive em Deep Learning), por isso vamos dar uma atenção maior a eles.
Perceptrons Multicamada
Um exemplo bastante popular de utilização dos Perceptrons Multicamada é na identificação de dígitos escritos a mão. Vamos abordar isso até para entender melhor a relação entre Redes Neurais e imagens!
Sem entrar muito nos detalhes técnicos por trás disso agora, entenda que, quanto mais camadas ocultas possuir, melhor capacidade a rede neural tem de interpretar padrões complexos dos dados de entrada. Isso faz sentido no caso de imagens, pois se você imaginar que as figuras acima estão representadas em tons de cinza e possuem resolução de 28x28, isso significa que cada imagem de entrada terá 784 dados de informação (são 784 pixels).
Imagine que nossa rede, inicialmente, só tem a capacidade de dizer se uma imagem contém o número zero ou não. Isso significa que são 784 nós na camada de entrada que não realizam cálculos, só "entregam" os pixels brutos para a camada oculta fazer o trabalho. Quando a camada oculta retornar os dados finais de saída, será uma probabilidade entre 0 e 1 que será retornada pelo nó de saída. Se o valor for maior do que 0,5, isso significa que a imagem inicial era realmente um zero. Caso contrário, não era mesmo um zero. Também é importante dizer que, nesse exemplo, a camada de saída possui um único nó de saída.
Pulamos a camada oculta até agora de propósito, não se preocupe. Queremos elucidar de maneira muito clara como se configuram as camadas de entrada e saída, antes de falar da parte mais complicada.
Você deve ter percebido que precisamos de um único nó de saída para identificar se é um zero ou não. E quanto ao 1, 2, 3, 4,...,9? Como fazer para nosso perceptron multicamada categorizar também os outros dígitos?
Se você pensou "adicionamos um nó de saída para cada possibilidade", então você acertou!
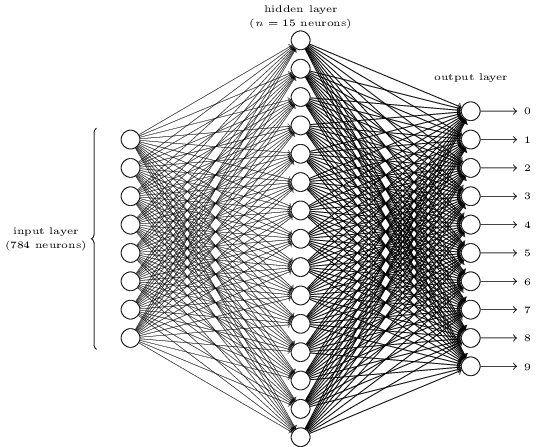
A arquitetura acima não é a única possível para resolver esse problema, mas essa funciona bem na prática. Na camada de entrada temos 784 nós de entrada (que obviamente não cabem na figura e por isso foram omitidos) e 10 nós de saída, um para cada dígito. Cada nó de saída informa uma probabilidade entre 0 e 1, e o nó com a maior probabilidade é, de fato, o nó do dígito identificado.
Ao olhar a camada oculta, você deve estar intrigado pensando em porque temos 15 neurônios na mesma e o que cada um deles está fazendo. Resumidamente, todos os neurônios dessa camada recebem os dados da camada de entrada (os pixels, que normalmente são valores normalizados em que 0 é a cor preta, 1 é o branco e 0,5 é o cinza médio, por exemplo). A seguir, os neurônios da camada oculta "dividem" o trabalho, de forma que cada um analisa um agrupamento de pixels em busca de um padrão.
Você pode imaginar, por exemplo, que o primeiro neurônio da camada oculta (o que está no topo) está procurando um padrão como o da imagem abaixo:
Da mesma forma, suponha que os três próximos neurônios da camada oculta estão em busca, respectivamente, dos seguintes padrões:

Para seguir num exemplo didático, suponha que os quatro neurônios acima encontraram aqueles padrões e "dispararam" informações que levaram ao nó de saída obter o maior para um nó associado a todos esses padrões: o zero. A imagem de entrada, no caso, é essa que está abaixo:
Assim sendo, o exemplo acima ajuda a entender um pouco o que a camada oculta faz. Ela busca, simultaneamente, diversos padrões associados com cada possível nó de saída (e, logicamente, seu dígito). Até por isso, é bem difícil interpretar o que um perceptron multicamada está inferindo de possíveis regras para dizer que um dígito é 3 ou 7. Dependendo da forma que a rede neural é inicializada, isso pode alterar bastante os padrões buscados pelos nós da camada oculta.
"Tudo muito bom, Lucas, mas como o neurônio da camada oculta sabe quais padrões ele deve procurar?"
Ótima pergunta! Isso é feito durante o treinamento dessa rede neural. Vamos falar sobre isso.
Treinamento do Perceptron Multicamada
Definir quais padrões devem ser procurados em um neurônio de uma das camadas ocultas já é parte do que é fazer uma rede neural "aprender". Esse processo ocorre pelo treinamento e ele tem muitos detalhes técnicos. Até por isso, a ideia é explicar de um jeito mais simples aqui e passar fontes para você se aprofundar (elas estão ao final do post).
Antes de começar, de maneira similar ao SVM que citamos no texto passado, precisamos criar uma pastinha no computador para cada rótulo (no caso aqui, é cada dígito possível). Assim teríamos a pastinha pro 0, pro 1, pro 2, pro 3 e assim sucessivamente, até o 9. Dentro de cada uma dessas pastas, colocaríamos uma série de imagens escritas a mão referentes ao dígito.
Basicamente o treinamento do Perceptron Multicamada (e de redes neurais profundas de maneira geral) consiste em três etapas, que em inglês são: forward pass, calculate error e backward pass. Traduzindo da nossa maneira, seria algo como: propagação pra frente, cálculo de erros e propagação pra trás.
Antes de explicar melhor essas etapas, vamos imaginar uma analogia que explique razoavelmente o que é feito.
Analogia do Treinamento (Aprendizado) da Rede Neural
Imagine que você é presidente de um país. Para ilustrar esse exemplo, escolhi o Tallis Obed Moses, líder de Vanuatu.
Você deve estar se perguntando porque escolhi esse cara. É que eu queria um presidente pra ilustrar o exemplo e eu não queria que fosse nenhuma pessoa conhecida pelo público brasileiro, para não ser taxado de esquerdista ou direitista.
Mas enfim, imagine que o sr. Moses acaba de se tornar presidente de Vanuatu. Para fins de exemplo, esqueçam que Vanuatu tem um primeiro-ministro.
Inicialmente, ele não conhece direito seu eleitorado e seu objetivo maior é manter sua rejeição a menor possível. Para isso, o sr. Moses precisa fazer escolhas.
Cada escolha que ele faz tem impacto no eleitorado. Se ele aumentar os impostos entre os mais ricos, a classe média e pobre não só não repudiarão como deverão ficar mais satisfeitos, pois foram poupados. Se ele aumentar a repressão contra o tráfico de drogas, por exemplo, partes do eleitorado reagirão de formas diferentes. No final, o que importa é a rejeição final que ele terá.
A única certeza que ele tem são as escolhas de seus antecessores. O sr. Moses tem relatórios anotados com tudo que os que presidiram antes fizeram e ele tem mais ou menos ideia do impacto de suas escolhas. Isso ajudará ele a se nortear, mas é claro que ele vai ter que se arriscar.
Assim, com o tempo, sr. Moses tomará decisões que farão o eleitorado como um todo reagir de maneira positiva ou negativa. Ao final, ele verá se sua rejeição aumentou. Se isso tiver ocorrido, ele irá refazer seus passos para entender qual foi a decisão que levou a isso e, se tiver como, tentar desfazer um pouco dessas ações para ver se estanca ou até mesmo recupera parte da aprovação. Sr. Moses sempre fará isso de maneira gradual e controlada, pois sabe que movimentos extremos deverá ter efeitos extremos na sua popularidade.
Assim, ele sempre seguirá os seguintes passos:
Tomará a decisão, verificando o impacto em sua rejeição.
Analisará sua rejeição para ver se melhorou e piorou.
Baseado no efeito dessa popularidade, ele vai "calibrar" suas ações, tentando reverter o que puder para sempre minimizar sua rejeição total.
O sr. Moses sempre repetirá as 3 ações acima: tomará a atitude, verá o efeito na sua popularidade, aprenderá esses efeitos e calibrará suas ações, com o objetivo de sempre empurrar sua rejeição para baixo. Basicamente é um método de agir, ver o efeito e voltar atrás se necessário, sempre usando esse feedback em seu favor, aprendendo com ele.
E a Rede Neural Artificial?
Ela fará basicamente a mesma coisa. Ela irá começar fazendo classificações praticamente "no chute". A seguir, vai analisar o quanto errou e quais neurônios produziram essas imagens classificadas incorretamente (voltando ao exemplo dos dígitos). Lembre-se que já "entregamos" para a rede neural quais são as classes (os dígitos) os quais aquelas imagens pertencem. Com esse feedback, a rede como um todo vai "calibrar" seus neurônios para que desfaçam esses erros ou mesmo não os repitam mais.
É um "pingue e pongue" de tentar classificar e se ajustar, classificar e se ajustar... que repetido milhares ou milhões de vezes, vai acabar encontrando as regras que fazem ela acertar com todos os dados que conhece (as imagens de seu treinamento).
Para entendermos melhor esse procedimento, precisamos de mais alguns detalhes que omitimos até agora: cada neurônio das camadas ocultas possui um peso associado (wi), uma entrada associada advinda da camada de entrada (xi, poderia ser o valor dos pixels entre 0 e 1, por exemplo) e um bias (valor este que é o mesmo para toda a camada oculta). Os pesos wi estão associados as entradas xi, como mostra a figura abaixo (que destaca um neurônio da camada oculta para ilustrar).
Se tivéssemos uma imagem com apenas 4 pixels, a saída que o neurônio acima apresentaria é mostrada abaixo:
Sendo f a função de ativação logística, que é uma conta bem enjoadinha rs (nesse texto tem detalhes sobre ela e outras funções que podem ser usadas nos neurônios). Leia também esse aqui, dá uma boa base matemática de tudo que estou falando nesse texto.
Assim sendo, a etapa de "propagação pra frente" consiste nas subetapas listadas abaixo:
Para cada imagem de treinamento (que já sabemos de antemão qual dígito é, como se tivéssemos um gabarito) nós "alimentamos" os nós de entrada com seus pixels. É importante lembrar que a rede neural processa uma imagem inteira por vez.
Os dados são recebidos pelos neurônios da camada oculta, que vão, inicialmente, procurar padrões aleatórios. Num primeiro momento, os cálculos dos neurônios serão bem ruins.
A saída de cada neurônio oculto representada pela função logística, por exemplo, será repassada aos nós de saída, que apresentarão uma probabilidade de 0 e 1 para cada possível dígito. O nó cujo dígito possui a maior probabilidade é o dígito daquela imagem.
Feita a "propagação para frente" usando todas as imagens de treino, chegamos na fase de "computar erros", que consiste em verificar o total de erros cometidos pela rede neural naquele intervalo. Para isso, computamos uma equação chamada função de custo (mais detalhes sobre ela aqui). Queremos que essa função dê sempre o menor valor possível, pois quando o valor dela é alto, significa que muitas imagens do treino estão sendo classificadas incorretamente (por exemplo, dizendo que uma imagem com um 0 na verdade é um 8).
Como já sabemos de antemão o dígito de cada imagem (como se fosse um gabarito), fica fácil verificar que há erro e, assim, somá-lo para a função de custo. Discrepâncias muito grandes somam valores altos para a função de custo; quando a rede classifica corretamente, então pouco ou nada é somado para ela.
A medida que a função de custo vai se aproximando de zero, isso significa que a rede neural está conseguindo classificar corretamente as imagens.
O fato é que, num primeiro momento, a função de custo dará um valor alto. Quanto mais imagens tiverem diferença entre o dígito real para o dígito predito pela rede, mais elevado é o valor da função de custo. A única forma de fazer a rede "acertar" mais da próxima vez, é ajustando os valores de wi para os neurônios e de b para as camadas ocultas. Lembre-se que cada peso wi e bias b definem os padrões que estão sendo analisados e, consequentemente, qual será o dígito classificado pela rede na camada de saída.
Dessa forma, chegamos na etapa de "propagação para trás" (backpropagation), que já é um pouco mais complicada. Basicamente uma rede neural é capaz de minimizar uma função, e a função que ela está analisando no momento é a sua função de custo. O valor final dela depende de cada peso wi e bias b. Modificando esses valores, reduzimos o valor final da função de custo. Conseguir fazer isso é, ao mesmo tempo, fazer os neurônios identificarem os padrões certos.
Basicamente quando a rede neural erra, ela verifica de onde veio o erro do neurônio propagado e "devolve" essa diferença (propaga ela para trás), para que o mesmo ajuste seu peso wi (ou mesmo o bias b de toda a camada) de forma a "calibrar" esse erro e não cometê-lo da mesma forma (ou evitar isso ao máximo).
Essa é uma forma bem simplificada de resumir. Aqui entra um pouco de cálculo diferencial para que ela possa saber "a direção" do erro e do acerto, via método do gradiente. Não vou explicar isso aqui, pois na teoria, esse texto é para qualquer um ler. O que não impede que, no futuro, seja feito um texto que continue esse aqui. No futuro gostaria de estudar isso mais a fundo e realmente explicar a matemática por meio do texto e de código. Se você tiver pressa para saber esses detalhes, saiba que o sentdex (canal no YouTube) está fazendo uma série e um livro em que ele vai programar redes neurais "na unha", sendo essa uma baita oportunidade para aprender.
Precisamos de muitas camadas ocultas?
Talvez, em um primeiro momento, você pense por quais motivos precisaríamos de uma, duas ou mais camadas ocultas. Será que ter 20 camadas ocultas é melhor do que 10 ou 5? Quanto mais camadas do tipo, melhor é a classificação?
Essa escolha tem a ver com a complexidade dos seus dados de entrada. O exemplo da compra de carro, por exemplo, é muito simples. Uma única função "separa" os dados em dois conjuntos. Você deve se lembrar de algo parecido que falamos no texto passado.
Vamos tentar introduzir um pouco de matemática aqui de um jeito interessante: existe um tal de "Teorema da Aproximação Universal" que fala algo bastante útil. Em seu livro de Deep Learning, um dos pais das Redes Generativas Adversárias, o Ian Goodfellow, disse que:
Lendo esse trecho uns tempos atrás, descobri essa informação que eu desconhecia: uma rede neural com uma única camada (imagine algo sem uma camada de entrada ou saída, mas apenas uma camada cheia de neurônios) é capaz de representar qualquer função. Assim, teoricamente, poderíamos resolver qualquer problema de classificação em que nosso conjunto de dados é capaz de ser “separado” entre funções.
O problema disso é que precisaríamos de mais neurônios do que o necessário, e como vimos na explicação acima, isso aumentaria o erro propagado em toda a rede. Isso ocorre pois, com mais neurônios, mais “unidades de processamento” esmiuçando os dados de entrada teríamos. Cada uma introduz erros.
Fora que, se o número de neurônios for muito maior do que o necessário, você vai ter neurônios procurando padrões muito específicos de seus dados, fazendo com que o aprendizado se ajuste tanto aos dados ao ponto que acaba generalizando mal pro universo do problema.
O ideal é que o número de camadas ocultas não seja pequeno demais nem muito grande. Existem algumas formas de se estimar isso e, quando não se tem certeza do número de camadas e neurônios, testa-se exaustivamente diferentes quantidades, até se descobrir a combinação que leva ao melhor resultado. É normal rodar diversos experimentos de redes neurais durante dias ou semanas =)
Para concluir…
Muita coisa ficou de fora desse texto, mas acho que consegui colocar o mínimo possível para se ter alguma noção do que Redes Neurais Artificiais fazem para aprender e, dentre uma série de coisas, classificar adequadamente. Elas também são usadas em outros problemas, que espero poder explicar em futuras oportunidades. Com essa base, acho que fica mais fácil dizer no próximo texto como usamos isso para o reconhecimento facial.
Pode ser que algumas perguntas tenham ficado em aberto. Vou respondê-las de uma vez:
Quando uma Rede Neural pode ser considerada Deep Learning?
Existem arquiteturas muito diferentes entre si que são Deep Learning, mas em geral, quando a arquitetura possui mais de uma camada oculta, ela já é considerada Deep Learning. Isso inclui algumas arquiteturas que também são Perceptron Multicamada.
O quão boa é a Rede Neural que resolve o problema de identificar dígitos escritos a mão?
Como mencionamos lá em cima, uma das possíveis arquiteturas para resolver esse problema é a da imagem abaixo:
Só que apesar dessa rede ser bastante robusta, obtendo mais de 90% de acurácia, ela ainda não resolve o problema eficientemente como uma Rede Neural profunda (a de cima, apesar de grande, só tem uma camada oculta, o que não a torna Deep Learning de fato).
Ela usa a base de dados MNIST que contém mais de 60 mil imagens de treino, 10 mil para os testes e que os melhores resultados são obtidos por redes neurais convolutivas. Esse paper aqui, por exemplo, consegue obter apenas 0,23% de erro no conjunto de teste.
No próximo texto espero falar de redes neurais convolutivas e, finalmente, como elas são aplicadas em detecção e reconhecimento de faces. Até lá! =)