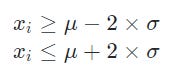Como Detectar Outliers de Forma Simples com Python e Pandas
Nesse texto explico uma maneira simples de identificar informações não comuns em sua base de dados.
Temos um projeto de extensão no Instituto Federal do Sudeste de Minas Gerais - Campus Rio Pomba que consiste em catalogar dados referentes a óbitos, casos confirmados, recuperados, etc de COVID-19 nas cidades da região de Juiz de Fora e Ubá. Essas informações encontram-se disponíveis em um painel no site www.covidmg.com.
No entanto, como os dados são inseridos manualmente por voluntários a partir de boletins de diversas prefeituras, pode ocorrer de alguns dados serem cadastrados imprecisamente. Outra possibilidade é da informação obtida ser bem anômala, o que nos obriga a analisar o que houve para esse dado estar tão diferente dos outros. Dessa forma, um jeito simples de se verificar esse tipo de coisa é por meio da identificação de outliers (pontos discrepantes).
Nesse texto mostro como eu fiz isso para esse projeto de um jeito relativamente simples em Python. Apresentarei isso com exemplos e com código-fonte disponível no Google Colab.
O que são Outliers?
Sabe aquela coisa de "ponto fora da curva"? Pois então, quando você tem um conjunto de pontos e um deles está representado numa posição bem diferente dos demais, temos um caso de outlier.
Na figura acima temos um gráfico com um outlier assinalado. Fonte: MATLAB RECIPES FOR EARTH SCIENCES.
Detectar outliers é algo bem importante em Data Science, pois eles podem estar associados a anomalias que precisam ser descobertas. Por exemplo, se tivermos uma série de batimentos cardíacos de uma pessoa ao longo de muito tempo, outliers podem indicar uma potencial doença cardíaca.
No caso de um histórico de transações com cartão de crédito, qualquer uso incomum pode ser um indício de fraude, que se identificada a tempo, pode proteger clientes e bancos.
No contexto do projeto de painel para COVID-19, dados discrepantes podem ser um indício de alguma informação de óbitos, casos confirmados, suspeitos, descartados ou outros com algum problema. Não que seja o caso sempre, mas pode fornecer um indicativo. Por isso, é importante que essa análise seja levada em consideração e feita de maneira não supervisionada por um algoritmo.
Todo o código desenvolvido no contexto desse tutorial encontra-se aqui.
Carregando a Base de Dados
Atualmente eu acesso uma URL que gera um arquivo JSON. Não achei apropriado disponibilizar para não sobrecarregar o servidor. Assim, pode-se baixar esse arquivo aqui contendo os dados que usei para esse tutorial. Ele é uma lista em Python salva como um arquivo binário.
Inicialmente, o código abaixo disponibiliza uma interface que permite a você fazer upload do arquivo baixado acima.
from google.colab import files
uploaded = files.upload()
for fn in uploaded.keys():
print('User uploaded file "{name}" with length {length} bytes'.format(
name=fn, length=len(uploaded[fn])))Ao clicar “Escolher arquivos” acima, você deve selecionar o arquivo covidmg.list baixado anteriormente.
Um upload bem sucedido aparecerá assim.
A seguir, o código abaixo converterá o arquivo binário covidmg.list em uma estrutura de dados Lista no Python, chamada covid_list. Para quem não conhece, a biblioteca Pickle é capaz de gravar estruturas de dados como listas ou instâncias de classes em um arquivo binário. Daí você pode salvar essas informações em disco e carregar em seu código quando precisar.
import pickle
with open ('covidmg.list', 'rb') as fp:
covid_list = pickle.load(fp)Agora vamos transformar essa lista em um dataframe do Pandas. O Pandas é uma biblioteca muito útil para fazer Análise de Dados. Para identificar outliers, ela será bem apropriada.
import pandas as pd
#construtor que vai criar um dataframe vazio, já contendo as colunas da base de dados do projeto
df = pd.DataFrame(columns = ["nomeMunicipio", "dataCaso", "confirmadosCaso", "recuperadosCaso", "obitosCaso", "suspeitosCaso", "descartadosCaso"])
#laço for que vai percorrer cada elemento da lista e inserí-lo como uma linha desse dataframe
for e in covid_list:
df_line = pd.DataFrame([[e["nomeMunicipio"], e["dataCaso"], e["confirmadosCaso"], e["recuperadosCaso"], e["obitosCaso"], e["suspeitosCaso"], e["descartadosCaso"]]], columns = ["nomeMunicipio", "dataCaso", "confirmadosCaso", "recuperadosCaso", "obitosCaso", "suspeitosCaso", "descartadosCaso"])
df = df.append(df_line)
#imprimir as 10 primeiras linhas
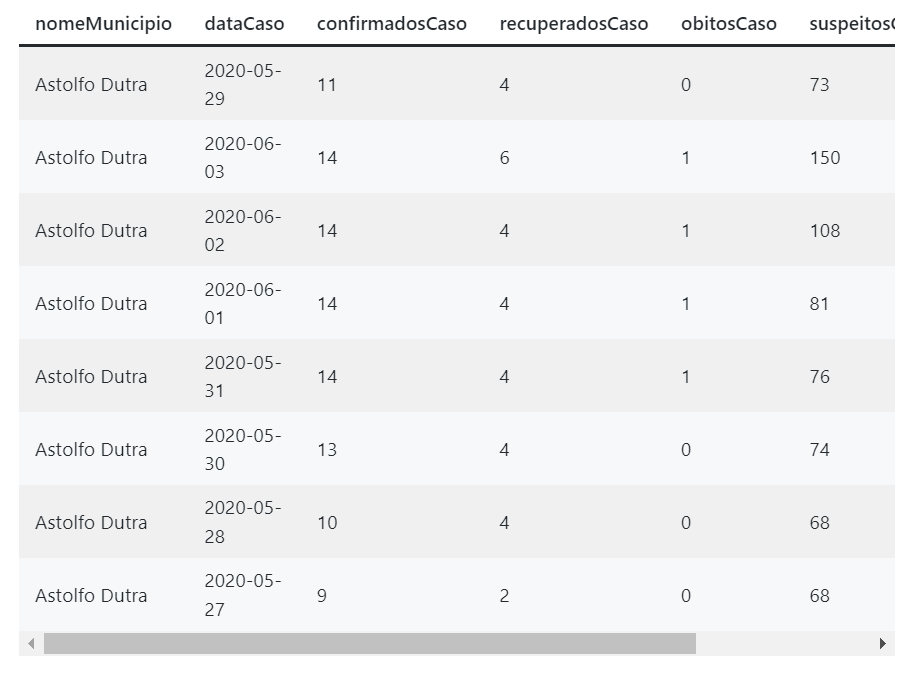
df.head(10)Eu gosto de pensar que o dataframe é como se fosse uma tabela, contendo registros. Cada linha é uma informação da base de dados, que no contexto desse tutorial, será a inserção de informações referente aos confirmados, recuperados, óbitos, suspeitos e descartados por COVID-19 para um dia qualquer em uma determinada cidade.
Abaixo eu mostro as 10 primeiras linhas desse dataframe, para fins de exemplo.
Preparando Dados
Para entendermos como procurar esses pontos discrepantes na base de dados, vamos analisar uma cidade dessa base que tenha registros inseridos com erro, que é o caso de "São Geraldo".
cidade = "São Geraldo"
#a linha abaixo constrói um novo dataframe só contendo registros da cidade listada acima
df_cidade = df.loc[df['nomeMunicipio'] == cidade]
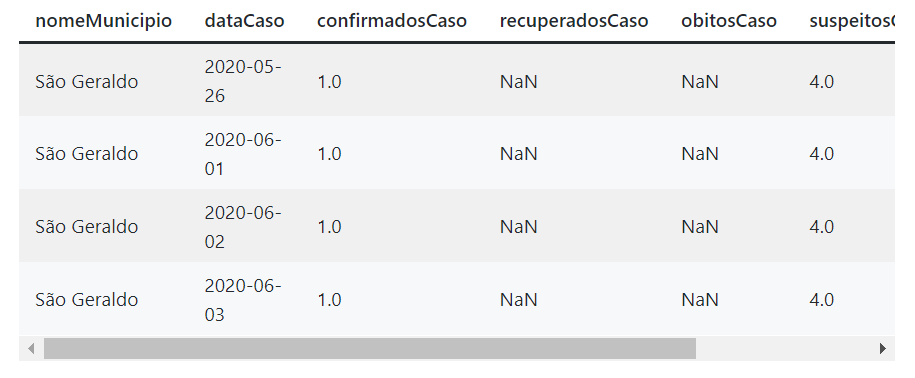
Exemplo de um possível segmento do dataframe gerado acima.
Ao obter os dados, alguns problemas podem ser notados. Além do NaN (Not a Number, basicamente o Python nos informando que o valor alí guardado é indefinido), as datas estão em formato de string. Podemos então converter esses dados aos tipos corretos via Pandas: float e datetime.
#converte coluna pro tipo datetime
df_cidade['dataCaso']= pd.to_datetime(df_cidade['dataCaso'])
#converte as colunas numéricas para float (ponto flutuante de 32 bits)
df_cidade["confirmadosCaso"] = pd.to_numeric(df_cidade["confirmadosCaso"], downcast="float")
df_cidade["recuperadosCaso"] = pd.to_numeric(df_cidade["recuperadosCaso"], downcast="float")
df_cidade["obitosCaso"] = pd.to_numeric(df_cidade["obitosCaso"], downcast="float")
df_cidade["suspeitosCaso"] = pd.to_numeric(df_cidade["suspeitosCaso"], downcast="float")
df_cidade["descartadosCaso"] = pd.to_numeric(df_cidade["descartadosCaso"], downcast="float")Um Pouco de Teoria
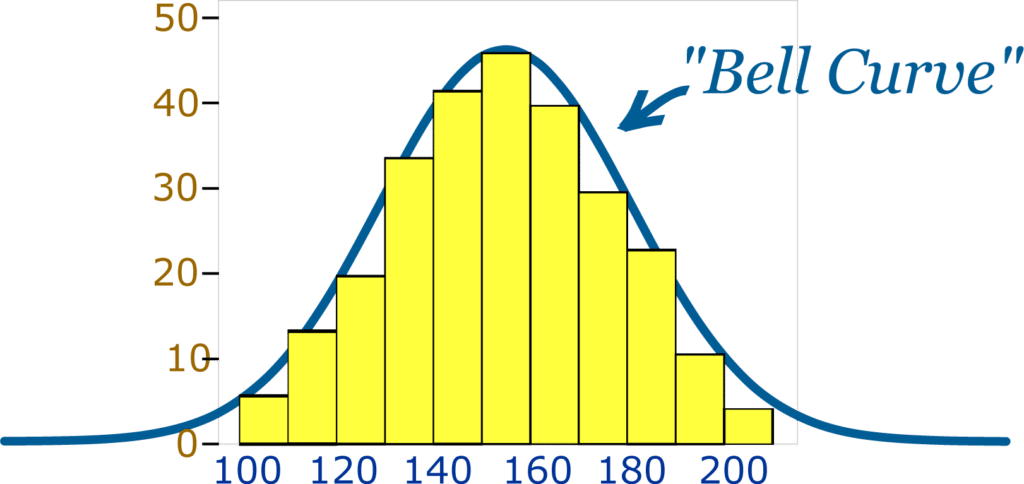
É muito comum no campo da Estatística que um conjunto de dados com alguma homogeneidade tenha seus pontos muito concentrados em torno da média. Isso faz com que assumam a forma de uma "montanha" ou "sino". Esse tipo de distribuição costuma ser chamada de distribuição normal ou distribuição gaussiana.
Exemplo de uma distribuição gaussiana, em que a maior parte dos pontos se concentra entre os valores 140 a 160.
No exemplo acima, a média aparenta estar em torno do valor 150, já que a maior parte das amostras concentra-se nessa posição. À medida que o valor vai aumentando ou diminuindo, ele vai se tornando incomum. Assim, podemos ver que poucos exemplos possuem valores em torno de 100 ou 200. Com isso, eles vão se tornando pontos não tão usuais, obtendo características de outliers.
Assumindo que nosso conjunto de dados assuma o formato de uma distribuição gaussiana, podemos fazer uso de algumas definições matemáticas para automatizar a detecção de anomalias. Além da média, considere a definição de desvio padrão.
O desvio padrão nos diz o quanto os dados variam (divergem) em relação à média. Para entender isso, considere dois conjuntos:
Grupo A: Seis alunos com as idades: 13, 14, 12, 13, 15, 14
Grupo B: Seis pessoas com as idades: 12, 5, 60, 44, 25, 40
O primeiro conjunto tem média:
O segundo conjunto tem média:
Enquanto a média do Grupo A é um bom indicador da idade dos alunos, vemos que a média do Grupo B é pouco informativa. Apesar da sua média ter sido 31, nenhuma das pessoas do grupo possui 30 anos!
Tudo isso é mostrado na fórmula de desvio padrão. Ela é computada da seguinte maneira:
Subtraímos cada elemento pela média ao quadrado;
Somamos tudo;
Dividimos pelo total de elementos;
Aplicamos a raiz quadrada.
Para o grupo A:
Para o grupo B:
Assim, enquanto o grupo A pouco varia em relação a média (devio padrão abaixo de 1), temos que o grupo B possui uma dispersão grande (de praticamente 19 anos em relação à média).
Usando a Média e Desvio Padrão para Detectar Outliers
Existem muitos métodos para se detectar outliers e os mais simples consideram o desvio padrão e a média. Explicarei aqui o chamado z-score.
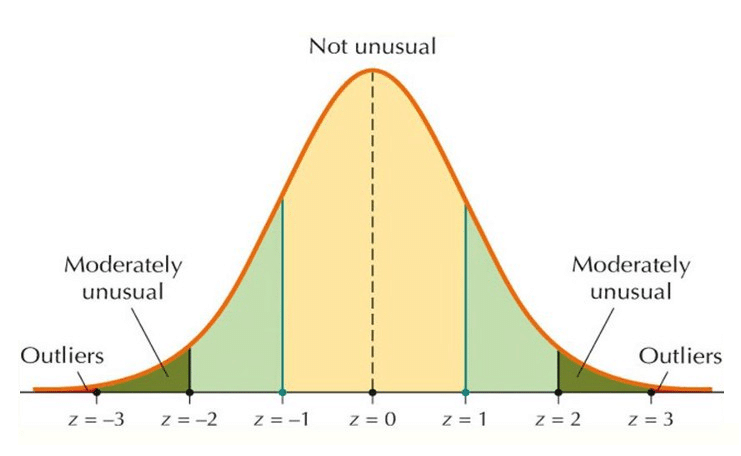
Em uma distribuição normal, espera-se que as amostras estejam próximas da média. À medida que se afasta da média, o ponto corre um sério risco de ser considerado outlier.
Assim, considerando o gráfico acima, é esperado que as amostras xi de uma distribuição normal estejam no intervalo entre:
Em outras palavras, se a amostra xi estiver entre o intervalo da média subtraído pelo desvio padrão multiplicado por dois e a média somada com o desvio padrão multiplicado por dois, então pode ser considerada usual.
Agora, se a amostra for:
ou
Aí ela será considerada muito fora dos padrões e, portanto, um outlier. No entanto, dependendo da base de dados usada, 2 pode ser um limiar melhor a ser multiplicado pelo desvio padrão do que 3. Isso porque, em geral, as amostras da distribuição costumam estar no intervalo da média vezes o desvio padrão multiplicado por 3 (ao menos em 99,7% dos casos).
Dito isso, vamos aplicar essas ideias em Python.
Identificando Outliers em Python
Primeiramente, vamos considerar o dataframe de uma cidade qualquer e computar a média e o desvio padrão de suas informações.
#calculando desvio padrão da cidade
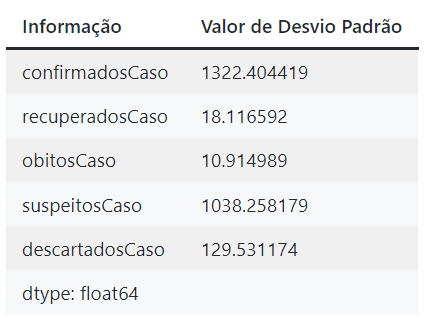
cidade_std = df_cidade.std(axis = 0, skipna = True) #skipna = True faz com que os possíveis valores NaN (not a number) inválidos sejam ignorados
cidade_stdExibição dos valores de desvio padrão computados pelo código acima.
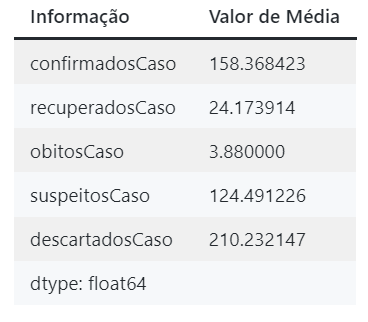
Similarmente, vamos computar a média das informações para a mesma cidade.
cidade_mean = df_cidade.mean(axis = 0, skipna = True)
cidade_meanExibição dos valores de média computados pelo código acima.
Nesse momento eu preciso computar os limiares de mínimo (média subtraída pelo desvio padrão vezes 3) e de máximo (média somada pelo desvio padrão vezes 3) para todas as informações acima.
#multiplico o desvio padrão de cada informação por 3
threshold = cidade_std * 3
#obtenho os limiares de mínimo e máximo pra todas as informações
lower = cidade_mean - threshold
upper = cidade_mean + threshold
#imprimo os limiares na tela
print("Lower limit:",lower)
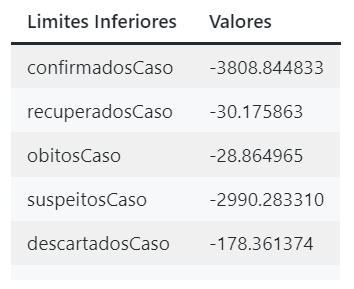
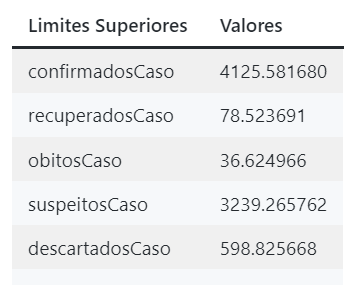
print("Upper limit:",upper)Abaixo eu apresento os resultados em um exemplo dos prints acima, tanto para os limites superiores quanto inferiores.
Valores dos limites inferiores computados.
Valores dos limites superiores computados.
No entanto, é importante observar que cada problema tem suas particularidades. Sabemos que não é razoável esperar que o número de casos confirmados ou óbitos, por exemplo, sejam negativos. Então qualquer valor abaixo de zero já pode ser considerado um outlier e, assim, 0 é um bom limite inferior.
Finalmente, agora basta buscarmos valores em nossa base de dados que estejam fora do intervalo de amostras esperadas.
#A linha abaixo retorna o número de amostras acima do que seria esperado (outlier)
df_cidade.loc[df_cidade["confirmadosCaso"] > upper["confirmadosCaso"]]
#A linha abaixo retorna o número de amostras abaixo do que seria esperado (outlier)
#lembre-se que no contexto da covid, o ideal é que o limiar seja zero =)
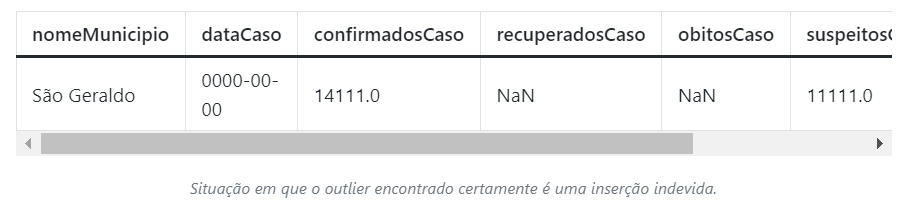
df_cidade.loc[df_cidade["confirmadosCaso"] < lower["confirmadosCaso"]]Ao executar o código acima, encontramos um registro que ultrapassa e muito o limiar superior e que certamente é um cadastro incorreto.
Conclusão
Existem diversas técnicas para se detectar outliers, especialmente considerando o tipo de distribuição dos seus dados. No entanto, para o contexto de distribuições gaussianas, o método de Z-Score pode ser bastante útil, como foi no exemplo.